Através dos números – Função quadrática e parábolas

Olá 🙂

Como dito no primeiro post, a falta de contextualização entre a matemática e o mundo real faz com que muitos não vejam sentido em aprendê-la. Nesse post, vamos descobrir a aplicação de um dos temas da álgebra no nosso dia-a-dia, começando com uma simples matéria de ensino médio: função quadrática.

Também chamada de função polinomial do 2° grau, a função quadrática representa algo muito presente a nossa volta. Não vamos nos ater a como resolver, já que para isso há diversos tutoriais pela internet. Vamos apenas relembrar algumas coisas e ver através dos números.

O que é função quadrática

De forma resumida, função quadrática é uma função de 2° grau que representa parábolas. Seus primeiros registros encontrados no antigo (bem antigo) Egito, indicam que inicialmente foram criadas para cálculo de divisão de terras (que nem sempre eram quadrados retinhos) de herança.

São de 2° grau porque são cálculos voltados para coisas de duas dimensões (como áreas de um terreno) e por sua vez, a potência máxima para x é 2 (de x²) o que resultará em dois resultados para X. Assim, x não pode ser elevado a 3 (x³), porque aí seria uma função cúbica e aí é outro assunto.

Uma equação de segundo grau possui o seguinte formato:

A função f(x) = 3x² + 2x – 5 é um exemplo de função quadrática, assim como f(x) = –x² + x – 1. Para resolver esse tipo de função (e com “resolver” quero dizer “encontrar os valores de x”), é necessário encontrar os três valores, a, b e c. Para isso é só observar a função:

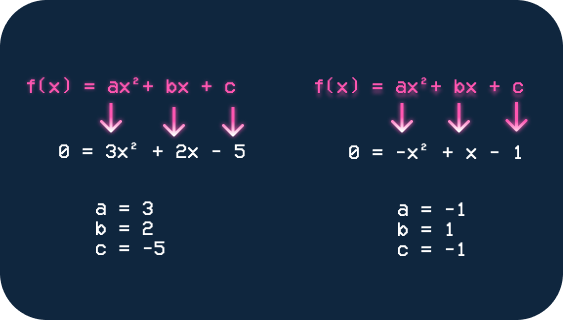
Depois disso, é só jogar os valores na fórmula de bháskara:

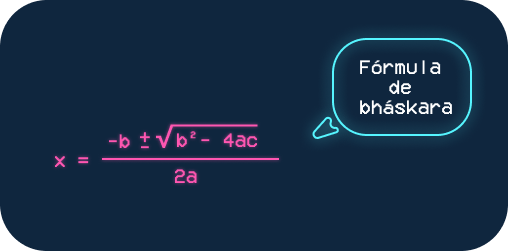
Após resolver a fórmula de bháskara, chegaremos em dois resultados; dois valores para x que nos ajudarão a desenhar uma parábola. Não vamos detalhar aqui o passo a passo da resolução desse cálculo, mas no final do artigo tem uma surpresa para facilitar sua vida :).

Função quadrática e parábolas

Como foi dito, toda função quadrática representa uma parábola. O que é uma parábola? É uma curvinha:

Quando o primeiro valor da função, o a, é maior que zero, a parábola fica virada para cima, já quando a é menor que zero, a parábola fica virada para baixo. Se for igual a zero, então não é função quadrática.

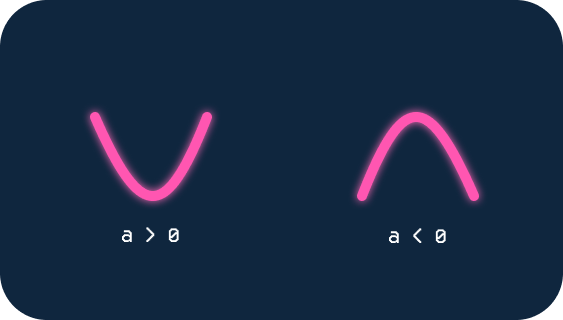
Usando os exemplos anteriores, a função 3x² + 2x – 5 = 0 geraria uma parábola parecida com a da esquerda da imagem acima (a = 3, a > 0), enquanto que a parábola da função –x² + x – 1 = 0, seria parecida com a da direita (a = -1, a < 0).

Existem outros parâmetros que nos ajudarão a desenhar melhor a parábola, como o valor de delta, mas até aqui está de bom tamanho.

Parábolas pelo mundo

Vimos até agora que uma parábola pode ser traduzida matematicamente usando uma função quadrática. Mas onde estão essas parábolas no mundo real? Veja alguns exemplos:

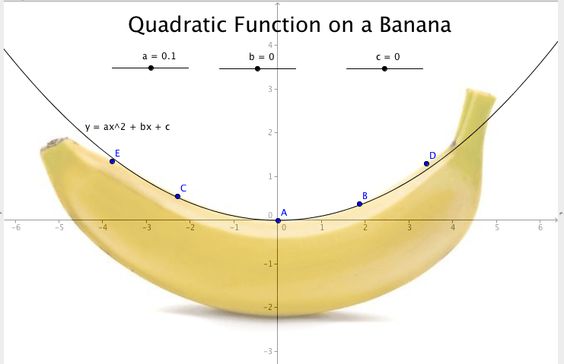
Uma banana 🤣 tem formato parabólico, assim como o movimento que a bola de basquete faz:

Em engenharia, o formato da parábola é visto em construções como pontes, montanhas-russas, etc:

Aos poucos, vamos percebendo que elas estão por toda parte. Na minha opinião, é muito bonito olhar para essas formas e lembrar que ali existe matemática.

Qual a utilidade das parábolas?

“Ok, Sawa. Entendi o que uma função quadrática representa e entendi sobre parábolas, mas qual a utilidade delas? É só uma curva!” – talvez você me questione.

As parábolas são relevantes para áreas da engenharia e da física. Qual sua utilidade? Imagine que a curva da parábola possui um pico, que chamamos de vértice, que é o ponto mais alto (ou o mais baixo) da curva. É o ápice da parábola. A existência desse vértice é a chave para entendermos a funcionalidade de uma parábola. Guarde esse detalhe e observe os exemplos a seguir.

Antena parabólica

Uma antena parabólica reflete todo o sinal vindo do espaço, que vem em diversas direções. Mas graças ao formato parabólico, todo o sinal acaba se concentrando no centro (ou no vértice) da antena. O ponto focal, o vértice, unifica todo o sinal recebido.

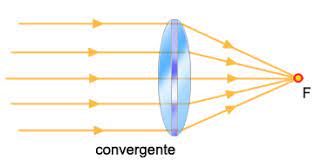
Lente de aumento

Já usou uma lupa e a luz do sol para botar fogo em algo? A lente de aumento possui um formato côncavo, uma parábola muito mais sutil que uma antena parabólica, mas não deixa de ser uma. Por que uma lupa é capaz de atear fogo? Porque, como parábola, ela possui um vértice, um ponto focal, que concentra todo o calor do sol que chegou na lente. Ao amplificar o calor por concentrá-lo num único ponto, fica fácil botar fogo.

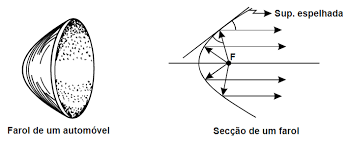
Farol de carro

O farol de um carro nada mais é do que uma lâmpada no meio de uma estrutura parabólica espelhada. Se você prestou atenção até aqui, percebeu que a parábola consegue unir tudo o que chegou nela para um ponto focal, como se fosse um funil. O farol de carro consegue projetar a luz para frente graças ao espelhamento dentro da parábola onde a lâmpada se encontra:

E não para por aqui, há radares, trajeto de mísseis balísticos, satélites e mais um monte de projetos que aproveitam dessa utilidade das parábolas.

Além das curvas

Além de calcular áreas e coisas em formato côncavo, a função quadrática também é utilizada para cálculos de lucro empresarial.

Em matemática financeira, o cálculo permite aferir preços e lucros (ou prejuízos) de mercadorias. Geralmente é usado para encontrar o lucro máximo que um produto pode dar.

function bhaskara(){
   if(a === 0){
      alert("Valor de a não pode ser zero =/. ");
      return;
   }

   var a =  prompt("Valor do coeficiente a:");
   var b =  prompt("Valor do coeficiente b:");
   var c =  prompt("Valor do termo independente c:");

   var delta = Math.sqrt((b*b) - 4*a*c);

   var x1 = parseFloat(((-b + delta) / 2*a).toFixed(4))
   var x2 = parseFloat(((-b - delta) / 2*a).toFixed(4))

   alert("O valor das raízes são:"+ x1 +" e "+ x2);
}

bhaskara();